这是一个美国的Python网络数据分析代写
PROBLEM 1: Network Measures (10%)
In this problem you will analyze a real-world network modeling academic collaborations.
The real-world collaboration network is provided in collaboration_edges.txt. Nodes in this
undirected network represent authors of research papers on the arXiv in the General Rel
ativity and Quantum Cosmology section. There is an edge between two authors if they
have co-authored at least one paper together. Note that some edges may appear twice in
the data, once for each direction Ignoring repeats and self-edges, there are 5242 nodes and
14484 edges.
1.1 Degree Distribution
Let pk be the degree distribution of a network. pk gives us the probability that a ran
domly chosen vertex has degree k.
(i) Plot the degree distribution on a log-log scale. In other words, generate a plot
with the horizontal axis representing node degrees and the vertical axis repre
senting the proportion of nodes with a given degree (by “log-log scale” we mean
that both the horizontal and vertical axis must be in logarithmic scale). Add the
plot to your written submission. No code submission required.
(ii) In one to two sentences, describe the degree distribution of the collaboration
network and it’s implication on how researchers working on general relativity
and quantum cosmology collaborate.
1.2 Clustering Coefficient Recall that the local clustering coefficient for a node vi was
defined in class as
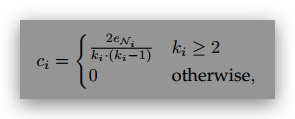
where ki is the degree of node vi and eNi is the number of edges between the neigh
bors of vi. The average clustering coefficient is defined as
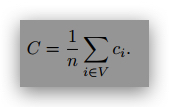
(i) Compute and report the average clustering coefficient of the collaboration net
work. No code submission required.
(ii) In one to two sentences, explain what this entails about collaboration practices
of researchers publishing about general relativity and quantum cosmology.
PROBLEM 2: Network Models (25%)
One of the goals of complex network analysis is to understand the characteristics of real
world networks. One way to gain more insights is to compare them to statistics we can
derive or compute for networks generated from mathematical models. In this problem, we
will explore two famous models—Erd˝os-Rényi and Small World—and compare them to
the statistics of the real-world academic collaboration network computed in the last prob
lem. Note that in this problem all networks are undirected.
• Erd˝os-Rényi Random graph (G(n; m) random network): Generate a random instance of
this model by using n = 5242 nodes and picking m = 14484 edges at random.
• Small-World Random Network: Generate an instance from this model as follows: begin
with n = 5242 nodes arranged as a ring, i.e., imagine the nodes form a circle and
each node is connected to its two direct neighbors (e.g., node 399 is connected to
nodes 398 and 400), giving us 5242 edges. Next, connect each node to the neighbors
of its neighbors (e.g., node 399 is also connected to nodes 397 and 401). This gives us
another 5242 edges. Randomly Finally, randomly select 4000 pairs of nodes not yet
connected and add an edge between them. In total, this will make m = 5242 × 2 +
4000 = 14484 edges. (You will have to write your own code to construct instances of
this model.)
• Real-World Collaboration Network: Reuse your computations from the last homework.


