本次加拿大作业是关于MATLAB 随机过程相关的一个MATLAB代写Assignment
Consider a simplified digital channel in which the transmitter sends signal
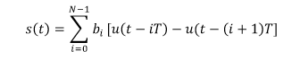
where 𝑏! is the i-th bit of information. Assume that the signal is randomly generated so that each bit can be modeled as a binomial random variable taking value of 0 with probability p and value of 1 with probability 1-p.
On the receiver side, the channel is sampled at times
𝑡’ = 𝑗𝑇 +𝑇/2 where j=0,….,(N-1)
Due to the presence of electrical interference the received signal is corrupted by additive Gaussian noise with zero mean variance 𝜎(. Therefore, the received signal at the sampling time is given by
𝑟5𝑡’6 = 𝑠5𝑡’6+𝑒(𝑡’)
where each noise sample is with zero mean variance 𝜎(. The noise samples at different times are independent Gaussian random variables. Once the signal is received the channel decoder makes a decision on what signal was sent using the following decision rule
Where we use symbol (hat) above s to denote that this is a decision affected by the channel noise and is referred to as an estimate of the sent symbol.
In the absence of any noise (ideal scenario) 𝑠)
8 = 𝑏’. In reality, due to the noise presence, an
error can be made. There are two types of possible errors: 𝑠)
8 = 0 when 𝑏’ = 1 and 𝑠)
8 = 1 when
𝑏’ = 0.
Task 1: Find the pdf of the received signal 𝑟(𝑡’) and the pmf of the estimated sent signal 𝑠’ assuming 𝜏 = 0.5 and 𝜎( = 0.25.
Task 2: When the variance of the additive noise is too large the probability of making errors will increase. Using MATLAB simulate (i.e. generate a sequence consisting of 1000 randomly generated bits, corresponding received signal and estimated signal) the above channel using p=0.5 and 𝜏 = 0.5 for the following noise variances: 0.1, 1, 10, 100. Compare the values of 𝑠̂5𝑡’6 and 𝑏! and count how many errors (both types) are made on a sequence consisting of N=1000 bits. Plot the probability of error as a function of noise variance.
Task 3: Select randomly a word from your textbook. Convert the letters in these words to their ASCII values and then to the binary representation of the corresponding ASCII values. Let us use the corresponding binary values as your input signals 𝑏!.
For example, McMaster converts to 77 99 77 97 115 116 101 114 and consequently in bit representation to 01001101 01100011 01001101 01100001 01110011 01110100 01100101 01110010 (in total 64 bits).
Using the channel from Task 2 transmit the selected word through the channel using following values 𝜏 = {0.25,0.5,0.75} and 𝜎( = {0.1,1,10}. Identify how many letters were decoded incorrectly for each of the scenarios. Does the number of correctly decoded letters depend on tau and sigma? Justify your answer.


