本次英国代写是一个Matlab流体力学的assignment
Instructions:
The purpose of this coursework (CW) is to demonstrate your ability to apply numerical methods to
solve problems in chemical engineering, particularly in fluid flow. This CW will contribute 30% to the
final mark. You are allowed to use any software of your choice such as Matlab, Python, Excel, C, C++,
Fortran, etc. The most important aspect that will be assessed is your ability to investigate and implement
the numerical solutions needed to solve the problem and explain the outcome in a concise technical report.
In Matlab and Python, there are several in-built methods and libraries to solve numerical problems. In this
coursework, however, you have to implement your own numerical methods. The quality of the scientific
writing will also be assessed as well as the quality and discussion of the results (Tables, Figure, Equations,
use of English language, etc).
Problem 1. Potential flow in a square channel
In this problem, you will have to make use of a concept in fluid mechanics known as Potential flow.
Potential flow is an ideal flow that does not actually represent any real phenomena, but it is an important
model that provides a good approximation to several real applications. The main idea in potential flow is
that a so-called potential function φ exists such that the velocity field is given by
V~ = rφ (1)
For this problem, write a technical report describing the following points.
(i) Investigate and provide a brief description of the main characteristics of potential flow, and demon
strate that the continuity equation for potential flow becomes the so-called Laplace equation.
[5 marks]
(ii) Consider now the geometry in Figure 1(a), in which an incompressible fluid enters a two-dimensional
channel with a uniform velocity U1. The fluid then finds a square obstacle which reduces the area
in half and the fluid leaves with a uniform velocity U2. Assuming the flow can be described using
potential flow, describe how the flow will behave in this system. You can assign numerical values
(the specific values are arbitrary and your own choice) to the variables L1, L2, U1, and U2.
[10 marks]
(iii) To determine and visualize the stream lines in this system it is necessary to solve the Laplace equation
for the geometry shown in Figure 1. For this, it is possible to use the method known as \Finite
differences”. To apply this method, the space is discretised using a square grid as the one shown in
Figure 1(b). Write a computer program in the language of your choice to solve the Laplace equation.
Explain clearly your boundary conditions for this problem and the implementation of the numerical
method.
[50 marks]
(iv) Visualise the stream lines (potential flow lines) and the velocity profile using a surface map plot.
[20 marks]
(iv) Discuss the results obtained from your numerical analysis.
[15 marks]
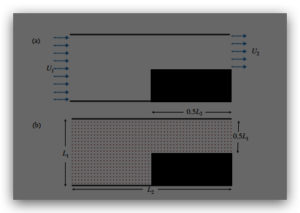
Figure 1. (a) Geometry of a two dimensional channel with an obstacle. The fluid enters with an uniform vecloity
U1 and leaves the channel with a uniform velocity U2. (b) Example of a square grid used to solve the Laplace
equation using the finite difference method.


