本次美国代写是一个Matlab计量经济的限时测试

1. data1945 2015.mat(for question 1)

(a) data: The raw dataset.
(b) date: Years from 1945 to 2015.
(c) dividend: Dividend.
(d) price: Price data from S&P500 index.

2. Q2.mat(for question 2)

(a) data: The raw dataset.
(b) date: Quarters from 1947Q1 to 2017Q4.
(c) sp: S&P500 return.
(d) crsp: CRSP value-weighted return
(e) cons: Real consumption expenditures per capita nondurables plus services.
(f) cc: Cyclical consumption from the full sample.
(g) log excess crsp: log CRSP value-weighted excess return.
(h) log excess sp: log S&P500 excess return.
(i) log crsp: log CRSP value-weighted market return.
(j) log sp: log S&P500 market return.
(k) rf: Risk-free rate.
(l) infl: Inflation.

3. GW predictors m524.mat

(a) GW predictors m524: The macro dataset of Goyal and Welch from 1947Q1 to 2017Q4.
(b) log DP: Log dividend-price ratio.
(c) log DY: Log dividend yield.
(d) log EP: Log earnings-price ratio.
(e) Svar: Stock Variance.
(f) BM: Book-to-market ratio.
(g) NTIS: Net equity issuance.
(h) TBL: Treasury bill rate(annualized).
(i) LTY: Long-term yield(annualized).
(j) LTR: Long-term return.
(k) DFY: Default yield spread(annualized).
(l) DFR: Default return spread.

1. Suppose you want to estimate β using OLS from the following model finite sample t =
1, 2, · · · , T, with assumed joint normality of the error terms as shown below. Estimator is βˆ.

We already know from lectures on Stambaugh’s estimator that the model creates a bias in
the estimation of the slope coefficient(also for intercept) when the data has high ρ and δ.

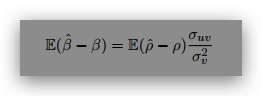
Consider another predictive regression bias-corrected slope estimator by Lewellen(2004, JFE).
The main idea behind it is that the largest possible bias(worst case scenario) occurs when ρ
is equal to one, as xt is considered to be not explosive so it is a good choice for maximum
value. Therefor, he proposes a conservative estimate of the bias-corrected slope conditional

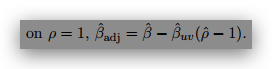
We want to test the hypothesis using the test statistic given below and the standard normal
critical values(two-sided, 5%) under the null of no predictability H0 : β0 = 0. For the given
annual dataset data1945 2015.mat, use them to define the continuously compounded return
rt, as discussed in class, and the log of dividend-price ratio and use it as xt. Its one-period
lag is xt−1 and its average ¯ xt−1.

(a) Write the code to calculate βˆadj = βˆ−βˆuv(ˆ ρ−1). The correct answer is 0.02646(rounded).

(b) Write the code to calculate Qtest. The correct answer is 1.4352(rounded). Can you
reject the null? What about when we choose 10% significance level?