这是一个Matlab无线通信的作业代写
1 Write True/False with a brief justification. Make assumptions
where necessary and state them clearly: (6 X 5 = 30)
A: In QAM based wireless communication, the number of symbols per second (baud rate) is a function
of the available bandwidth.
B: In QAM based wireless communication, the number of bits per symbols is a function of the available
bandwidth.
C: OFDM communicates over N orthogonal frequencies (called subcarriers), hence it must use N an
tennas, one for each frequency.
D: Consider a wireless MAC protocol with random counter based channel access. The utility of the
medium would first increase and then decrease as a function the number of nodes in the system.
E: With SleepWell, write true/false for each of the statements below with justification.
• Latency decreases
• Throughput increases
• Energy savings increase
F: Slot size for counting down in randomized backoff can be smaller than the maximum signal propa
gation delay in the network.
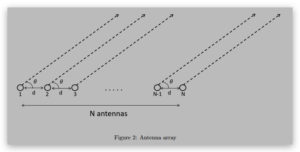
2 Beamforming-I (10)
Consider two antennas A and B separated by a distance of λ/2, and transmitting in-phase signals of
wavelength λ. A receiver R is placed on a line passing through the mid-point of the two antennas
and making an angle θ relative to them as shown in Figure 1. Determine the phase difference between
signals of A and B that arrive at R. Plot the phase difference as a function l, when l varies from 0 to
100λ (provide three plots for three different values of θ – 0, 90, and 45).
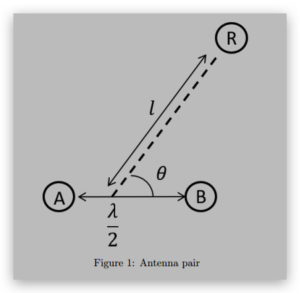
3 Beamforming-II (15)
Consider a uniform linear array of N antennas as shown in Figure 2. The antenna separation is d as
shown, and all antennas transmit signals in phase, at a wavelength of λ. Consider a receiver at an angle
θ very far away from the antenna array. Since the receiver is far, we can assume that lines joining the
antennas to the receiver are parallel to each other, making an angle θ above the horizontal line. Find
all angles θnull where the sum of arriving signals from all antennas add up to 0, creating a perfect null.