本次美国代写是一个Matlab随机过程的限时测试
Epidemic processes. The term epidemic refers to a phenomenon that is prevalent in excess
to what might be expected. It is most commonly used in the context of diseases and their
dissemination throughout a population – such as with malaria, COVID, bubonic plague, and
AIDS – but it is also at times used more broadly in other contexts, such as in describing
the spread of perceived problems in a society as well as (mis)information cascades in online
social media. Epidemic modeling is concerned with three primary issues: (i) understanding the
mechanisms by which epidemics spread; (ii) predicting the future course of epidemics; and
(iii) achieving an ability to control the spread of epidemics. Random processes and stochastic
modeling has an important role to play in this context.
The most commonly used class of continuous-time epidemic models is the class of susceptible
infected-removed (SIR) models. Consider a closed population of N elements, of which S of
those elements are susceptible to infection (called ‘susceptibles’), I elements are infected (called
‘infectives’), and R elements recovered and immune (or, alternatively, ‘removed’ if you prefer
sad endings and also want to account here for deaths). Naturally, because of the closed system
assumption one must have N = S +I +R: The reactions that define the SIR model describe the
infection of susceptibles, and the recovery with subsequent development of immunity (or death,
in any case removal) of infectives. As shorthand (symbolic) notation for the model we use
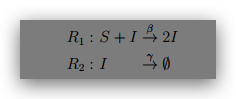
The first reaction R1 denotes infection of a susceptible element by chance encounter with an
infective. The rate of encounters between susceptible and infective individuals is specified to be β,
and is referred to as the infection rate. We will adopt the customary assumption of homogeneous
mixing among members of the population, which asserts that the population is: (i) homogeneous,
and (ii) well mixed, in the sense that any pair of members are equally likely to interact with
each other. Accordingly, for S susceptibles and I infectives the rate of reaction R1 is simply
βSI. Reaction R2 denotes recovery and immunity of an infective individual, and the recovery
rate is specified to be γ. For a population of I infectives, the rate of reaction R2 is thus γI.
This exam is roughly divided in two sections. In the first section, which comprises parts
A-E, you are asked to simulate a deterministic model for the population dynamics of the SIR
epidemic. In the second section, which comprises parts F-M, you are asked to build and analyze
a more realistic stochastic SIR model based on a continuous-time Markov chain (CTMC), and
determine the probability that the epidemic dies out. Note that each part may have multiple
questions, so read carefully to make sure you answer all questions.
A) Deterministic SIR model (10 points). Towards studying the dynamics of the SIR epidemic
process, for given continuous time instant t let S(t) be the number of susceptibles, I(t) be the
number of infectives, and R(t) = N − S(t) − I(t) be the number of removed elements in the
population. Consistent with the reactions R1 and R2, the deterministic SIR model is given by
the following system of nonlinear differential equations



