这是一个英国的C++计算金融代写案例

1 Background

1.1 Stock Options

The trader has calibrated a specialised risk neutral process for some underlying stock price. Given the
current stock is S0, market prices indicate the risk-neutral distribution of the stock price at time t is given
by:

St ∼ N(f(S0; t); v2(S0; t)) (1)

for some calibrated functions f and v2.

If (1) describes the risk neutral distribution, then the formula to value a call option V with payoff

g(S)

at time t = T is given by

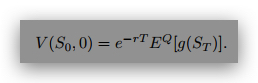
Then to carry out a Monte Carlo valuation of an option, we may use samples from a standard random
normal distribution

φ ∼ N(0; 1) (3)

to write the equation

ST = f(S0; T) + v(S0; T)φ: (4)

Equation (5) then generates a single random path, from which we can value a payoff

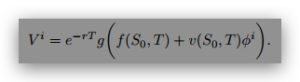
If n simulations are performed, then (as described in the notes) we merely average out the V i to yield
an approximation for the value of the portfolio, i.e.

then a Put Option V with a terminal condition

V (S; T) = max(X − S; 0)

written on the asset S has the analytic solution

where N(z) is the standard cummulative normal distribution.

1.2 Path Dependent Options

Now assume that the stochastic process follow a standard Geometric Brownian motion governed by
dS = (µ − D0)Sdt + σSdW:

Then the following options will depend on S(tk) which are the share prices at K + 1 equally spaced sampling
times t0, t1, …, tK with t0 = 0 and tK = T (unlike part (a), the computation cannot proceed from t = 0 to
t = T in one step). Full details are given the the lecture notes – but the important point to note is that

Sitk = Stik−1 exp[(r − D0 − 12σ2)(tk − tk−1) + σptk − tk−1φi]

to estimate the underlying asset values at each time, where each of the K increments dWk involves drawing
φk from a Normal distribution.