本次美国代写是一个集成电路的限时测试
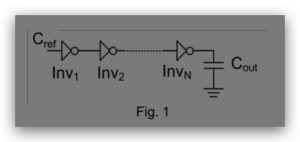
Problem 1: In this problem, you will choose the optimal number of stages and the optimal
sizing factor for the inverter chain shown in Fig. 1. You should assume that the input
capacitance of the first inverter is equal to that of the unit inverter (i.e., Cref). Also assume
that the parasitic capacitance at the output of the first inverter is Cint=Cref. Assume that the
delay of the unit inverter istr.
a) Derive the expressions for the optimal number of stages and the optimal sizing
factor.
b) If Cout = 750Cref, what are the optimal number of stages and the optimal sizing
factor for this inverter chain?
c) Using your answer to part (b), what is the optimal normalized delay (D) of the
inverter chain? Hint: normalized delay is defined as D=td/tr, where td is the
absolute delay of the inverter chain.
Problem 2 (Cadence). In this problem, you will implement problem 1 in Cadence using
FreePDK45.
a) Design and implement the minimum size inverter. Provide hand calculations to
describe your design methodology. What are the dimensions of the p- and n-type
transistors?
b) From the simulation results, compute the parasitic capacitance of the inverter (Cint).
Also compute the input capacitance (Cref) with the aid of simulations. How do these
capacitances compare?
c) Implement the inverter chain in Fig. 1 in Cadence to achieve the minimum path
delay. How does the optimal number of inverters compare with your calculations in
Problem 1? Please explain your observations.
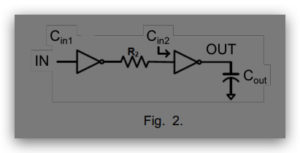
Problem 3. Consider the chain of just two inverters shown in Fig. 2, with a given Cout,
Cin1, and R2 = 3Req,1. Cin1 is the input capacitance of the first inverter and its value is equal
to its parasitic capacitance Cint1. Req,1 is the equivalent resistance of the first inverter.
Assume that Cout=100Cin1. What should the input capacitance of the second inverter (Cin2)
be to achieve the minimum delay?
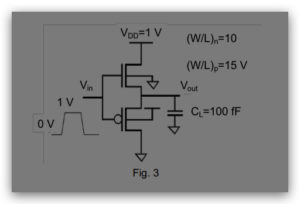
Problem 4: Consider the low swing driver of Figure 3 (use data in Table 1 for calculations).
a) What is the voltage swing on the output node (Vout)? Assume γ=0.
b) Estimate (i) the energy drawn from the supply and (ii) energy dissipated for a 0 V to
1 V transition at the input. Assume that the rise and fall times at the input are 0.
Repeat the analysis for a 1 V to 0 V transition at the input.
c) Compute tpLH (i.e., the time to transition from VOL to (VOH + VOL)/2). Assume the input
rise time to be 0. VOL is the output voltage with the input at 0 V and VOH is the output
voltage with the input at 1 V.
d) Compute VOH considering the body effect.