这是一个美国的计算复杂性assignment算法代写
1. Solve the following recurrence using the “Master Recurrence” (approximately slide 56 in the D&C slides).Clearly specify the constants a; b; c; d; k. You may assume that n is a power of 3:
![]()
2. Solve the recurrence given in the previous problem using the recursion tree/tabular method shown in lecture(approximately slides 49-55). You may assume that n is a power of 3. Try to give an exact solution, but a good big-O estimate is adequate if you can’t.
3. Let A and B be two arrays of length n containing numeric values, each array in sorted order. Give an O(log n) time divide-and-conquer algorithm to find the median of the set of 2n items in A [ B, where the median is defined to be the n-th smallest item in that union. For simplicity, you may assume that all values (in each array and between arrays) are distinct from each other, and you may assume that n = 2k + 1 for some integer k ≥ 0.
Give a brief English language description of your (recursive!) algorithm. Also write a clear pseudocode version of it. As outlined in the “Code to Recurrence” section of the D&C slides: Select the operations you want to count, and very carefully state exactly what they are. Annotate your pseudocode to highlighting the base case(s), recursive calls, and counted operations. Then write the corresponding recurrence relation. Use the “master recurrence” to solve it (approximately slide 56 in the D&C slides); clearly indicate what the constants a; b; c; d and k given in the master recurrence are for this problem. The emphasis this time is on analysis, but do include a brief correctness argument.
4. Give a fast divide and conquer algorithm for the following silhouette problem:
Input: an unordered list of triples (xl; xr; h), where 0 < xl < xr and 0 < h.
Problem: Each triple describes a rectangle of height h whose base is on the x axis, and whose left and right sides are at positions xl and xr, respectively. Imagine that each rectangle is opaque, and that the whole collection is illuminated from behind. The problem is to calculate the silhouette of the set of rectangles — a description of the visible edges in the resulting scene. (This is a very simple case of what’s called hidden line elimination in computer graphics.)
Output: A list of pairs (xi; yi), ordered by increasing xi, of the height yi at each point xi where the height of the silhouette changes. (See example below.)
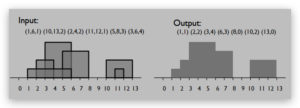
Unlike the example above, you may assume that all x coordinates are distinct and that n is a power of two. Your answer should address all points raised in the last paragraph of problem 3.
5. Multiply the 4-digit decimal numbers 2142 and 1233 using a Karatsuba-like divide-and-conquer algorithm similar to the one given in class for mutiplying binary numbers (i.e., with 3 multiplies of half-size integers per recursive level; base case is “table lookup” of 1-digit by 1-digit decimal multiplication). Show all steps. The usual “grade school” multiplication method requires 4 × 4 = 16 “base case” multiplies. How many did you need? The unnumbered slide following D&C slide 45 gives an example. If you choose to follow this model, don’t try to show all of thered/green arrows—too much clutter—but showing a few may make the pattern clearer.


