本次美国代写是关于信号分析相关的一个Assignment
Due before the start of your next lab. START EARLY!!! Upload your lab report, .m file(s), and Matlab Publisher files to Blackboard as described in the course syllabus.
PART 1: CONTINUOUS AND DISCRETE FOURIER TRANSFORMS (35 PTS)
In the first part of this lab, you will revisit the effect of sampling period on the Fourier Transform, but you will dig a little deeper this time to understand the relationship between the amplitude of a peak in the Fourier domain and the time-based signal that led to it.
1. Given a signal 𝑓𝑓(𝑡𝑡) = 5𝑒𝑒−0.2𝑡𝑡𝑢𝑢(𝑡𝑡) + 0.2cos(10𝜋𝜋𝑡𝑡), sampled at 5 kHz
a. In one figure, plot f(t) over 10 seconds. (1 pt)
b. In a second figure, create a 2×3 subplot. Row 1 will be results from the continuous Fourier transform. Row 2 will be the results from the discrete Fourier transform. Each column will represent a different sampling duration (period), T0. Let T0 for Columns 1-3 be 10, 50, and 100 seconds. (15 pts)
i. Plot the magnitude of the continuous Fourier Transform of f(t) (row 1) and the magnitude of the discrete Fourier transform (row 2) versus frequency for each of the T0 values. A couple of notes:
1. In your continuous plot, be sure to represent infinite values as an upward pointing arrow. To do this, you’ll want to determine where the infinite values are; the functions find(), subs(), or isinf() may help. You’ll also probably want to plot the arrows using the stem() command with “^” markers.
2. Be careful with your frequency domain units.
3. Don’t forget to account for ∆t in your FFT calculation.
4. Don’t forget about fftshift()
5. You may find it helpful to plot a narrower range of frequencies to better visualize the transforms.
6. Make sure all of your axes have the same limits so that you can easily compare plots.
c. Analysis:
i. Qualitatively, does the DFT correspond well with the corresponding theoretical continuous
Fourier transforms? (1 pt) ii. There are two components in your plots: a peak that does not change in amplitude and peaks that do change in amplitude with increasing T0.
1. Which part of f(t) produces each prt of your plots? (6 pts)
2. What is the mathematical relationship between the amplitude of the Fourier transform
(or FFT) and the exponential component of f(t)? (6 pts)
3. What is the mathematical relationship between the amplitude of the of the FFT and the sine wave component of f(t)? Tip: You may find it helpful to alter one coefficient at a time in f(t) to get a better idea of how each is contributing to the plots. (6 pts)
PART 2: PRACTICAL APPLICATION: EEG PROCESSING (65 PTS)
In the final part of this lab, you will analyze an artificial EEG signal. This question is a bit more open-ended and will require you to spend some time thinking about the proper way to analyze the signal. Your Minilab may provide you with a good first approach.
To start, download the data file ArtificialEEG.mat from Canvas. It will help to know that the signal was sampled at 1 KHz. The following table of frequencies associated with EEG will also be helpful.
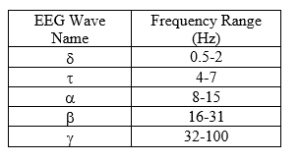
Remember, too, that it’s not uncommon for signals to be corrupted by noise. Sometimes this noise is a specific frequency and can be attributed to something. Later, in Lab 8, we’ll learn how to remove this type of noise. However, sometimes the noise can’t be attributed to anything and it contains several frequency components that are difficult to remove. You may see noise of a certain frequency and then harmonics of that frequency.
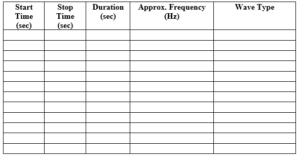
1. Analyze the signal. Provide all plots that you think help with your analysis. Discuss the underlying frequencies in the signal. Discuss when there are transitions in frequencies. Do you see all wave types? Are there any frequencies that are continuous? Over what times do you observe what frequencies? Do you observe any noise? If so, what type(s) of noise do you see, and when? You may find it useful to create a table (see below). (50 pts)
2. Find the dreaming states. (5 pts) Dream states are associated with lower amplitude and higher frequency EEG signals. Assume that EEGs over 75 Hz correspond to when your patient is dreaming. How many dreams did your patient have? When did it/they occur? How long did it/they last?
3. Noise. (10 pts) Discuss the noise in the system. When does noise occur? What types of noise do you see? Does the noise interfere with any of the signals in the EEG? If so, when and why? If not, why not? Do the results shown in your graphs make sense with respect to each other? Be as complete as possible in your answer.


