这是一篇来自澳洲的关于解决COMP 5416 Assignment 1问题的代码代写
Question 1 (Equilibrium of Three Competing Transmissions, 17%). Consider the following scenario where three mobile phones are competing to use the same channel. Each user independently decides either to transmit or not. There are 8 situations, and each user’s utility in each situation is listed below. If a user is the only one transmitting, she will get a utility of 10. If 2 or more users are transmitting simultaneously, no one is successful and all of them will get −5 utility. If a user is off, she will always get 0 utility. We aim to investigate the Nash equilibrium in this setting. Please note that in the presence of more than two users, Nash equilibrium is satisfied when no user can do better by unilaterally changing her own strategy. In this question,
Nash equilibrium is reached when the following conditions are all satisfied.
- If Users 2 and 3 do not change their strategies, User 1 cannot achieve a better utility by changing her strategy.
- If Users 1 and 3 do not change their strategies, User 2 cannot achieve a better utility by changing her strategy.
- If Users 1 and 2 do not change their strategies, User 3 cannot achieve a better utility by changing her strategy.
Consider the mix strategy, where p1, p2, and p3 denote the probabilities that Users 1, 2, and 3 are “on”. Calculate all possible values of (p1, p2, p3) when Nash Equilibrium is reached.
Hint: p1(1 − p2)(1 − p3) is the probability that User 1 is on and Users 2 and 3 are off.
Question 2 (Web Cache, 17%). Consider the following scenario where two schools of one university are installing web caches for users. (You only need to review the contents discussed in lectures in weeks 1–3 to complete this question.)
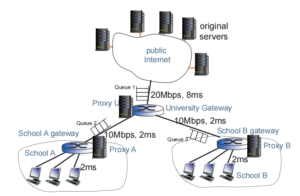
Inside each school, the one-way propagation delay from each host to the school’s gateway is 2ms. The link bandwidth is assumed to be infinity (sufficient large). The link bandwidth from each school’s gateway to the university’s gateway is 10Mbps, and one way propagation delay is 2ms. The access link bandwidth from the university’s gateway to the Internet is 20Mbps, and assume that the one-way propagation delay from the gateway to any server in the public Internet is 8ms.
On average, the requests from each school to view the webpage (of the public Internet) arrive at the rate of 1000 requests per second and the webpage is 1000 bytes (which fits exactly one packet). Ignore the header size. The requests themselves are very small and we assume that they do not take any bandwidth.
To analyse the delay, we model the system as there are three queues in the system: the downlink from the public Internet to the university’s gateway (Queue 1); the downlink from the university’s gateway to school A’s gateway (Queue 2); the downlink from the university’s gateway to school B’s gateway (Queue 3). In this question, we only consider the propagation delay (uplink and downlink) and the waiting time at the three queues (downlink only). For example, in Queue 2, the arrival rate is 1000 packets per second, and the service rate is 10 ×106 8000 = 1250 packets per second. The waiting time at the queue can be calculated as 11250−1000 = 0.004s= 4ms. You need to find out the waiting time by using the formula introduced in week 1, i.e.,1µ−λ . You do not need to know how this formula is derived at this stage).
(1) Without cache, what is the average overall delay for each user to derive its requested webpage? (Only the propagation delays and the waiting delays at the queues are considered. All other delays are ignored.)
(2) Now, caches can be installed at the school’s gateway, so that 10% of the original requests can be served by the schools’ proxies (proxies A and B). What is the average overall delay for each user to derive its requested webpage?
(3) Now, cache can be installed at the university’s gateway, so that 20% of the original requests can be served by the university’s proxy (proxy U). (There are no schools’ proxies.) What is the average overall delay for each user to derive its requested webpage?
(4) Now, caches can be installed at all gateways (proxies A, B, and U). a% of the original requests can be served by the schools’ proxies, and b% of the original requests can be served by the university’s proxy. However, due to the limited storage owned by the university’s ICT department, we have 2a% +b% ≤ 20%. Calculate the average overall delay for each user to derive its requested webpage as a function of a and b and find the optimal a and b. (Note, a% and b% are defined with respect to the original requests,do not use (1−a%)(1−b%), but to use (1−a%−b%) to calculate the rest of the requests served by the original Internet servers).3
Question 3 (Delay and Loss, 17%). As shown in the figure below, a file of size F = 1000 + S bytes is transmitted on an end-to-end connection over three links, where S is the last three digits of your student number. For example, if your student number is 490123456, then S = 456 and F = 1456 bytes.
Each link is 100 km. The signal prorogation speed is 2×108 m/s. Assume that a header of 28 bytes (UDP header and IP header) is added to each packet. The bandwidth of all links is R = 1 Mbps at the beginning. The nodes use the store-and-forward scheme. (Ignore processing delays at each node.)


